Triangle Area Calculator

  1. Kyle's Converter >
  2. Calculators >
  3. Geometry >
  4. Triangle Area

Triangle Area

For Triangles with Known Perimeter

Result:
6
Heron's Formula
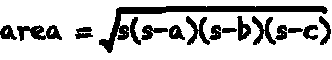side a units
side b decimals
side c    

A triangle with side a: 3, side b: 4, and side c: 5 units has an area of 6 square units.

This calculator and more easy to use calculators waiting at www.KylesCalculators.com
triangle area on chalkboard using heron's formula
 

Calculating the Area of a Triangle:

The area of any triangle with a known perimeter can be calculated according to Heron's formula as described below:

A = (s(s - a)(s - b)(s - c))^0.5
where s is half of the perimeter (semiperimeter).

Heron's formula is one of the most elegant solutions to finding the area of a triangle that doesn't contain a right angle.

(Triangles with a right angle or known altitude can make use of the simpler pythagorean theorem calculator.)

Heron's formula operates on any triangle where the length of each side is know. In Heron's formula, and most others, the sides of a triangle are typically denoted a, b , c. All other variables in the formula are calculated from these three measurements.

How to Calculate "s"

One calculated term is required to solve Heron's formula, it is half of the perimeter or a semiperimeter usually denoted by "s". Don't worry only the three side lengths are required to calculated the semiperimeter. As the name implies the calculation involves halving the sum of the length of the three sides.

In this example a semiperimeter is calculated for a sample triangle with side lengths 3, 4, 5.

  • s - (a + b + c)/2
  • = (3 + 4 + 5)/2
  • = (12)/2
  • = 6

Example of Using Heron's Formula to Find the Area of a Triangle

Try calculating the area of a triangle with side lengths 3, 5, 6. First calculate the semiperimeter as described above. Next follow the formula below. Note that ^0.5 means to take the square root of the calculation inside the parentheses.

  • A = (s(s - a)(s - b)(s - c))^0.5
  • = (6(6 - 3)(6 - 4)(6 - 5))^0.5
  • = (6(3)(2)(1))^0.5
  • = (6(6))^0.5
  • = (36)^0.5
  • = 6

What does an answer of "0" mean?

If the calculator gives an answer of zero (0) this means the resulting area is too small to be reported at the input precision level. Adjusting the precision from the drop-down menu will allow more decimal places to show and you may get an answer. However, if you were to visualize this triangle it would appear very thin, the area is imperceptibly small or maybe even nonexistant. Try calculating a triangle with side length 1, 2, 3. The result is zero because the resulting triangle has no area, it's really just a bunch of overlapping lines!

What does an answer of "NaN" mean?

An answer of "NaN" likely means your input side lengths cannot possibly form a triangle. If one side is too large relative to the length of the other two side a closed polygon will not be formed and the calculation will fail. No one side can be greater than the sum of the other two sides (it wouldn't be a triangle, the polygon wouldn't be closed)!